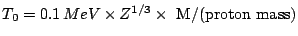SetCuts: conversion from range to kinetic energy
Charged particles
Starting from a particle cut given in stopping range, the method
constructs a vector holding the cut values in kinetic energy for every
material. The main steps of the algorithm are the same for all the
charged particles, the only difference is that different energy loss
formulae are used for electrons, positrons and heavy charged particles
(muon,pion,proton,...).
In the case of charged hadrons this procedure is applied for the proton
and antiproton only, the cut values in kinetic energy for other hadrons
are computed
using the proton and antiproton energy loss and range tables.
General scheme
- An energy loss table is created and filled for all the elements
in the element table.
- For every material in the material table the following steps are
performed:
- a range vector is constructed using the energy loss table and
formulae for the low energy part of the calculations,
- the conversion from stopping range to kinetic energy is performed and
the corresponding element of the KineticEnergyCuts
vector is set
(It contains the particle cut value in kinetic energy for the
actual material.),
- the range vector is deleted.
- The energy loss table is deleted at the end of the process.
Energy loss formula for heavy charged particles
The energy loss of the particle is calculated from a simplified Bethe-Bloch
formula if the kinetic energy of the particle is above the value:
The simplified here means that the low energy shell correction term and
the high energy Sternheimer density correction term have been omitted.
Below the energy value 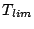 a simple parametrized energy loss formula
is used to compute the loss, which reproduces the energy loss values
of the stopping power tables fairly well. The main reason of using a
parametrized formula for low energy is that the Bethe-Bloch breaks down
at low energy. The formula has the following form :
a simple parametrized energy loss formula
is used to compute the loss, which reproduces the energy loss values
of the stopping power tables fairly well. The main reason of using a
parametrized formula for low energy is that the Bethe-Bloch breaks down
at low energy. The formula has the following form :
where : M = particle mass,
T = kinetic energy,
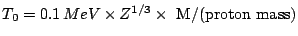
Z = atomic number.
the paramaters 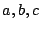 have been chosen in such a way that
have been chosen in such a way that 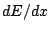 is a
continuous function of T at
is a
continuous function of T at 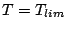 and
and 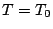 , and
, and 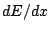 reaches its maximum
at the correct T value.
reaches its maximum
at the correct T value.
Energy loss of electrons and positrons
The Berger-Seltzer energy loss formula has been used for T 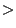 10 keV to
compute the energy loss comes from the ionization . This formula plays the
role of the Bethe-Bloch for electrons ( see e.g. the GEANT3 manual).Below
10 keV the simple c/(T/mass of electron) parametrization has been used,
where c can be determined from the requirement of continuity at T = 10 keV.
As in the case of electrons the radiation loss is important even at
relative low (few MeV ) energy, a second term has been added to the
energy loss formula which accounts for the radiation losses (losses due to
bremsstrahlung). This second term is an empirical parametrized formula.
For positrons a different formula is used to calculate the ionization
loss, the term accounting for the radiation losses is the same than that
for electrons.
10 keV to
compute the energy loss comes from the ionization . This formula plays the
role of the Bethe-Bloch for electrons ( see e.g. the GEANT3 manual).Below
10 keV the simple c/(T/mass of electron) parametrization has been used,
where c can be determined from the requirement of continuity at T = 10 keV.
As in the case of electrons the radiation loss is important even at
relative low (few MeV ) energy, a second term has been added to the
energy loss formula which accounts for the radiation losses (losses due to
bremsstrahlung). This second term is an empirical parametrized formula.
For positrons a different formula is used to calculate the ionization
loss, the term accounting for the radiation losses is the same than that
for electrons.
Range calculation
The stopping range is defined as :
The integration has been done analytically for the low energy part and
numerically above an energy limit.
Photons
Starting from a particle cut given in absorption length, the method
constructs a vector holding the cut values in kinetic energy for every
material. The main steps of the algorithm are the following:
- A cross section table is created and filled for all the elements
in the element table.
- For every material in the material table the following steps are
performed:
- an absorption length vector is constructed using the
cross section table
- the conversion from absorption length to kinetic energy is
performed and the corresponding element of the
KineticEnergyCuts vector is set
(It contains the particle cut value in kinetic energy
for the actual material.),
- the absorption length vector is deleted.
- The cross section table is deleted at the end of the process.
Cross section formula for elements
An approximate empirical formula is used to compute the absorption
cross section of a photon in an element.
The absorption cross section means here the sum of the cross sections
of the gamma conversion, Compton scattering and photoelectric effect.
These processes are the 'destructive' processes
for photons , they destroy the photon or decrease its energy.
(The coherent or Rayleigh scattering changes the direction of the gamma only,
its cross section is not included in the absorption cross section.)
Absorption length vector
The AbsorptionLength vector is calculated for every material as:
AbsorptionLength = 5/(macroscopic absorption cross section)
The factor 5 comes from the requirement that the probability of having
no 'destructive' interaction should be small, hence
Meaningful cuts in absorption length
The photon cross section for a material has a minimum at a certain kinetic
energy 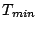 . The AbsorptionLength has a maximum at
. The AbsorptionLength has a maximum at 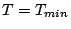 , the value of
the maximal AbsorptionLength is the biggest "meaningful" cut in absorption
length . If the cut given by the user is bigger than this maximum, a warning
is printed and the cut in kinetic energy is set to the maximum gamma energy
(i.e. all the photons will be killed in the material).
, the value of
the maximal AbsorptionLength is the biggest "meaningful" cut in absorption
length . If the cut given by the user is bigger than this maximum, a warning
is printed and the cut in kinetic energy is set to the maximum gamma energy
(i.e. all the photons will be killed in the material).
back
![\begin{displaymath}
\frac{dE}{dx} = \left \{ \begin{array}{ll}
a*\sqrt{\frac{T...
... & \mbox{for $T \in [T_0, \, T_{lim}]$}
\end{array} \right.
\end{displaymath}](img3.gif)